세그먼트 트리(Segment Tree)
세그먼트 트리는 주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위해 고안해낸 자료구조의 형태가 바로 세그먼트 트리다.
세그먼트 트리를 사용하는 이유는 구간 합을 할 때 데이터 업데이트가 느리기 때문이다.
구간 합을 통해 만들어진 합 배열에서 중간에 데이터가 바뀌는 순간 기존 데이터와 바뀌는 데이터의 차이 만큼 바뀌는 데이터 뒤에 위치한 값들에게 모두 더해줘야 하는 문제가 생긴다. 이러한 업데이트 시 시간이 오래걸린다는 문제점을 세그먼트 트리로 해결할 수 있다.
세그먼트 트리 핵심 이론
1. 트리 초기화 하기
리프 노드의 개수가 데이터의 개수 이상이 되도록 트리 배열로 만든다.
샘플 데이터로 {5, 8, 4, 3, 7, 2, 1, 6}이 주어진다면 먼저 트리의 크기를 구해야 한다.
트리의 크기를 구하는 방법은 2k >= N을 만족하는 K의 최솟값을 구한 후 2k * 2를 트리 배열의 크기로 정한다.
샘플 데이터는 총 8개로 2k >= N을 만족하기 위해 k는 3의 값을 가지게 되며 총 16의 크기를 가진 트리 배열이 만들어진다.


트리 배열을 만들면 샘플 데이터를 리프 노드에 넣어주는데 이때 2k를 시작 인덱스로 넣어주면 된다.

구간 합을 진행한다고 가정하면 구간 합을 뒤에서부터 시작해준다.

구간 합을 진행할 때 이진 트리 개념을 사용하여 부모 노드를 찾기 위한 N / 2를 사용하면 된다.
해당 예시에서는 2N을 사용하여 구했지만, 부모 노드의 값을 구하는 것이기 때문에 2 / N을 해도 같은 값이 나온다.

위의 과정을 반복해 합 배열을 완성시키면 위 사진과 같이 된다.
※ 노드 0은 없는 값이기 때문에 계산하지 않는다.
2. 질의 값 구하기
만약 문제로 주어진 질의 인덱스 범위의 구간 합을 구한다고 하면 여러 과정이 필요하다.
먼저 질의 인덱스를 세그먼트 트리 인덱스와 맞게 변환 해줘야 한다.
세그먼트 트리 인덱스로 변환하는 방법은 주어진 질의 index + 2k - 1이다.
문제로 위의 샘플 데이터에서 2~6에 해당하는 구간 합을 구하라고 가정해보자.
질의 값 범위를 세그먼트 트리 범위로 변환하면 9 ~ 13이 된다.
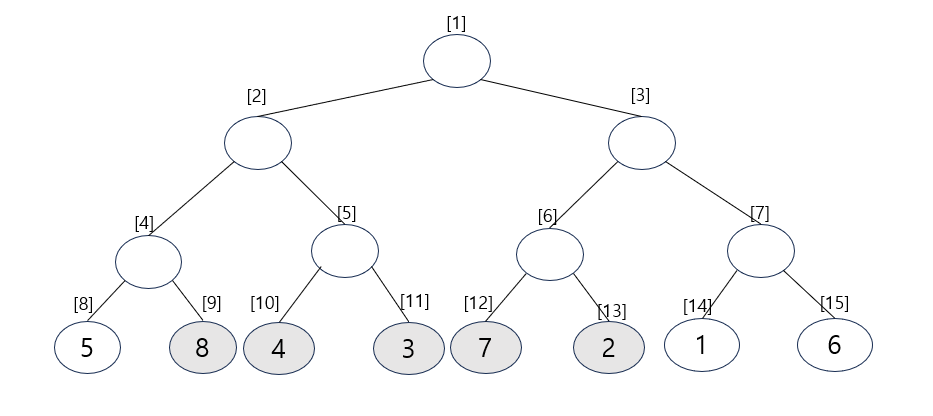
질의 값 구하는 과정
1. start_index % 2 == 1 일 때 해당 노드를 선택한다.
2. end_index % 2 == 0 일 때 해당 노드를 선택한다.
3. start_index depth 변경: start_index = (start_index + 1) / 2
4. end_index depth 변경: end_index = (end_index - 1) / 2
5. 1 ~ 4번 과정을 반복하다가 end_index < start_index가 되면 인덱스의 위치가 변경되기 때문에 종료한다.


현재 start_index가 9, end_index가 13이기 때문에 위의 과정에서 1, 2번을 수행하면 9번 노드는 선택하고 13번 노드는 선택하지 않는다는 것을 알 수 있다.
1 ~ 2에서 해당 노드를 선택했다는 것은 해당 노드의 부모가 나타내는 범위가 질의 범위를 넘어가기 때문에 해당 노드를 질의 값에 영향을 미치는 독립 노드로 선택하고, 해당 노드의 부모 노드는 대상 범위에서 제외한다는 뜻이다.

start_index인 9번 노드를 부모 노드인 4번 노드의 대상 범위에서 제거하여 질의 범위에 해당하는 부모 노드인 5번 노드로 이동한다.
여기서 부모 노드로 이동하기 위한 연산으로 index / 2가 아닌 (index + 1) / 2 와 (index - 1) / 2를 사용한 이유는 start_index가 어떤 부모 노드에서 왼쪽 리프 노드인지, 오른쪽 리프 노드인지 확인하기 위해서 사용하는 것이고 오른쪽 리프 노드에 속한다고 한다면 해당 부모의 범위에서 제외해야 하기 때문이다.
위의 예시와 같이 9번 노드에 해당하는 8의 값이 start_index에 해당하는데 자신의 왼쪽 리프 노드인 8번 노드는 질의 범위에 해당하지 않기 때문에 부모 노드인 4번 노드는 필요하지 않게 된다. 따라서 질의 범위에 해당하는 부모 노드로 이동이 필요하다.
마찬가지로 end_index에 해당하는 13번 노드를 살펴보면 (index - 1) / 2 연산을 수행해도 자신의 부모 노드인 6번 노드로 향하게 되기 때문에 별도의 부모로 이동 없이 사용하면 된다.
질의 범위인 9 ~ 13번의 총 합을 구하면 8 + 4 + 3 + 7 + 2 = 24가 되는데 4, 3의 구간 합인 7과 7,2의 구간 합인 9를 부모를 이동한 8과 더해주면 8 + 7 + 9 = 24로 같은 결과값이 나온다.
3. 데이터 업데이트 하기
앞서 언급한 것을 보면 세그먼트 트리를 사용하는 이유는 데이터 업데이트가 빠르기 때문이라고 했는데 어떻게 이루어지는지 살펴보자

3번 데이터의 값을 10으로 변경한다고 가정하자.
먼저 질의를 세그먼트 트리로 변환하면 index + 2k - 1 == 3 + 8 - 1 = 10이 되고 10번 노드에 해당하는 값을 변경해준다.
일반적인 합 배열에서 데이터 업데이트가 일어나면 기존 데이터와 업데이트되는 데이터 간의 차이를 해당 데이터 뒤에 나오는 각각의 합 배열 데이터마다 더해줘야 한다.
세그먼트 트리는 자신의 부모를 찾아가면서 업데이트 해주면 된다.

트리의 특성을 살려서 이진 트리가 부모로 이동할 때 / 2를 하는 것을 적용하면 된다.
'CS > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 그리디(Greedy) (0) | 2023.08.16 |
|---|---|
| 알고리즘 - 이진 탐색(Binary Search) (0) | 2023.08.16 |
| 알고리즘 - 최소 공통 조상(LCA, Lowest Common Ancestor) (0) | 2023.08.16 |
| 알고리즘 - 동적 계획법(DP, Dynamic Programming) (0) | 2023.08.15 |
| 알고리즘 - 조합(Combination) (0) | 2023.08.15 |
